CRIM uncertainty analysis

The results of investigation into combinations of Catchment Riparian Intervention Measures (CRIMs) have been previously presented. The figure below shows the location of the CRIMs throughout the Uck catchment. Those in red have a positive effect in terms of peak flow reduction. Those in yellow have a negative effect in combination!



Uncertainty analysis was carried out. The 52 positive sites (see previous post and results table) were the focus of this analysis. Essentially the roughness of the channel and floodplain along these reaches was varied in order to show how different levels of roughness effect the peak flow at Uckfield during the (simulated) 2000 flood event.




The key finding from the CRIM Uncertainty Analysis was that similarly fine results in terms of peak flow reduction at Uckfield can be achieved when channel Manning's n is ~0.10, as opposed to the default value for a CRIM of 0.14. This suggests a lower level of channel blockage is required for equally positive results.

HOWEVER, IMPORTANTLY, if channel n is only increased to ~0.10, floodplain roughness MUST be increased to a high level (Manning's n > ~0.16) in order to achieve the best results in relation to downstream peak flow.

Similarly, floodplain roughness can be much lower than 0.16, and providing channel n is high (> ~0.14), similarly fine results can be achieved.

it is important to note that this uncertainty analysis is only carried out for the 52 reaches identified from previous work, and will need to be repeated if different combinations of reach are selected.

Table 1: Results from exploration of effects of simulating CRIMs in combination on downstream peak flow (just upstream of Uckfield; based on 2000 flood event). Initial peak flow simulated for the 2000 event (no interventions) was 124.68 cumecs (2 d. p.). The ‘individual effect on peak flow’ is the effect on downstream peak flow of increasing roughness in that single reach. The ‘effect in combination’ is the simulated peak flow downstream as a result of the number of CRIMs added (shown in the final column).

Table 1

The effects of CRIMs applied in combination throughout the Uck catchment - uncertainty analysis to follow

As discussed previously, from the screening runs there are 127 reaches where increasing channel and floodplain roughness to simulate the adding on a Catchment Riparian Intervention Measure (CRIM) decreased downstream peak flow. It was decided that the 100 reaches with the greatest individual impact would be explored in combination.

Brief method:

Essentially for looking at CRIMs in combination I ranked the 100 reaches in order of how effective increasing channel and floodplain roughness (to simulate a CRIM e.g. debris dam and riparian vegetation planting) of that single reach in question, is on reducing downstream peak flow. So, for example the best reach reduces peak flow by ~3.5 cumecs when roughness is increased in just that reach.

A CRIM was simulated along the reach with the largest individual effect. Then a CRIM was also added to the reach with the second largest effect on downstream peak flow - a CRIM was therefore simulated in both of these reaches. If simulating a CRIM in these 2 reaches reduced downstream peak flow by more than simulating a CRIM in one reach both were retained in combination. I then simulated a CRIM in the third reach and so on. Each time a CRIM was simulated the cumulative effect on downstream peak flow was recorded. If simulating a CRIM in a new reach did not increase the positive impact (cumulative peak flow reduction was reduced) this reach was rejected and excluded from future combinations.

The results can be seen in the table accompanying this blog. Please give feedback on the quality of the table.


Issues

You can see from the table that the title 'reach applied (no.)' is highlighted yellow. These numbers are used in the model OVERFLOW to identify each reach and change, amongst other characteristics, roughness values. However they will have no meaning to those not using the model. Producing a figure with each reach numbered is not especially practical considering there are 234 reaches. This creates a bit of a problem for me in communicating the results, especially in terms of where I'm simulating an intervention.

There is also somewhat of a challenge in explaining the methods I have used; the process is likely to be very confusing to others. Hopefully the table will help you see the process I went through.

To think about/uncertainty:

As previously discussed, these results must be viewed with an appreciation of the uncertainty associated with the model and its inputs.

For looking at the combination of CRIMs I have ranked reaches primarily order of effect on peak flow. Whilst a consideration was made of reaches with a positive impact on the flood volume above approximate channel capacity this was not the focus. There may be reaches where increasing roughness reduces excess flood volume by a large amount, whilst having a slightly negative effect on peak flow; I will try and look at such reaches in some form.

The results presented here are for one combination of interventions. A different combination could suggest a different pattern of effects and different key reaches to focus on - this would reduce uncertainty of results/recommendations.

Is simulated roughness higher than might be expected from CRIMs in reality? I hope to get results from simulating the effects of increasing channel roughness by a smaller amount.

Again feedback is much appreciated, especially regarding any problems understanding the method or results, or issues with the presentation. I would like the blog to be as easy as possible to follow so results and the uncertainty can be understood.

New update on results soon...

New update on results soon...

Initial screening results from new calibrated model

As discussed the simulated hydrograph produced by the calibrated model shows a much better fit with the observed hydrograph from the 2000 flood event. In a few weeks (thousands of simulations takes quite a while) I'll be able to show more results on the uncertainty associated with the new calibrated model.

For now here are the initial screening results, similar to those presented a while ago for the old model.

A key aspect is the effect of placing a CRIM at one reach is greatly reduced. No reaches individually reduce flow peak by over 4 cumecs, as opposed to around 10 (depending on the time map used) which reduced peak flow by >5 cumecs with the old model.

One explanation for this is that the simulated peak discharge is more accurate and also lower. Therefore even if the CRIMs were still having the same effect in terms of % reduction of the initial flow peak, the reduction would be less.



Importantly, from initial work with combinations of reaches, it appears that in combination the reaches have less of a reducing effect on peak flow than the sum of their parts. For example, as a simplification, two CRIM sites which on their own reduce simulated peak flow by 3 cumecs each may in combination only reduce peak flow by around 4 cumecs.

These results will be discussed in more depth soon

Background to my project

Please see my first post for a brief context on my project, which will hopefully make the subsequent posts easier to follow for those not familiar with the work

Thanks, Ed

New model and new uncertainty

Following on from my results of the GLUE uncertainty analysis (see previous updates) the decision has been made to use a calibrated version of the Overflow model, with the aim of producing flood hydrographs which more closely match the observed hydrgoraph

Nick has been working hard producing a calibrated version of the Overflow model. The key different is a different rain time map (rainfall rate) is used throughout the storm event.

The result is a much closer match between the observed and simulated hydrograph at Isfield.

However there are are few issues with the new model;

The key issue is that when a hydrograph is simulated for the meadows area upstream of Uckfield, the largest flood peak now has a double peak. This is not expected and is slightly problomatic; the simulated peak discharge upstream of Uckfield now occurs only very slightly before the peak discharge at Isfield downstream, when perhaps a slightly bigger lag would be expected. If the peak were smoother, this would most likely bring the peak discharge just upstream of Uckfield forward a couple of hours.



On the positive side, the peak discharge is much more realistic.

As seems to be the way with modelling, as one aspect gets better, this can create a whole new set of problems. Just like a more comlex model can bring with it just as much uncertainty and a simple model.

Ill discuss the issue of the troublesome flood peak with Stuart Lane and I'm hoping that it wont be too much of a problem. The simulated hydrograph is now certainty much a closer fit to the previous uncalibrated model. Im looking forward to (hopefully) getting some final results I can properly work as time is running short in terms of my role in this study - I think we're all hopeful of some interesting results.

Whilst slightly frustrating to work on the previous model and then have to move on to a slightly different version, my previous work has allowed me to explore the behaviour of the model and get a better understanding of the uncertainties.


I have been now working on getting results of the screening runs (see previous updates) with the calibrated model, looking at the effects of increasing channel and floodplain roughness one reach at a time to represent the adding of a CRIM. Initial results to come...

Flood volume calculation: methods and uncertainties

In the previous update I mentioned the need to calculate the volume of water above the critical flood discharge i.e. the volume of water likely to spill onto the floodplain; a very important calculation when looking at the impact of a flood mitigation measure.

To do this, I essentially need to calculate the area of certain sections of a simulated flood hydrograph - the area under a graph. This is known as integration. The programme I am running my model in, MATLAB, allows this to be done in several different ways. However I am having problems using some of the available methods.

Therefore I am used the trapezoidal rule, which is not likely to give the most accurate estimate of the area of a graph;
http://en.wikipedia.org/wiki/Trapezoidal_rule

The following image is useful for understanding how the trapezoidal rule works
http://en.wikipedia.org/wiki/File:Trapezoidal_rule_illustration_small.svg

As it uses straight lines to approimate a curve, there are inevitably errors in area calculation - moreso than if I can use a similar but more accurate method - and therefore uncertainty in my findings. My aim is therefore to try to figure out how to use an improved method of integration. However, for the moment, the current does allow me to explore the effect of CRIMs on flood volume.

Initial results (for an uncalibrated model) on flood volume to follow soon....

Figure 1
A figure showing;
the oberserved flood hydrograph during the 2000 flood event (black).
the simulated flood hydrograph using a 30mm/day time map with no interventions(red)
the simulated flood hydrograph using a 30mm/day time map with a CRIM added along reach 127 (blue).
The figure shows how increasing the channel and floodplain roughness at reach 127 results in a decrease in flood peak of just over 3 cumecs (m3/s)
Important to note;
The observed hydrograph is taken from the Isfield gauge downstream of Uckfield, whereas the two simulated hydrographs produce hydrographs predicted for an areas just upstream of Uckfield. This will lead to a slightly greater difference between simulated and observed hydrographs

Screening simulaions - the effects of CRIMs; preliminary results

Screening simulations

These simulations involved increasing the channel and floodplain roughness along one reach at a time to simulate the adding of a CRIM (debris dam and floodplain vegetation) and looking at the impact this has on river discharge just upstream of Uckfield.

-NOTE- I will add some images showing some of my results in the next update, which I'll add after this.

Results have been produced for all rain time maps (1mm/day - 200mm/day). A potential problem I have is in deciding on an appropriate time map to use, as discussed in my previous update. It was mentioned that goodness-of-fit statistics can be misleading. Therefore I decided to look at the effect of CRIMs where time maps 30, 36, 42 and 50mm/day were applied.

- NOTE - The model may be calibrated with different time maps throughout the storm period.

My choice was based on what was felt to produce the best hydrograph when initially compared to the observed hydrgraph. As discussed previously, the hydrograph produced when using a 30mm/day time map shows an encouragingly good qualitative fit, albeit with a time lag.

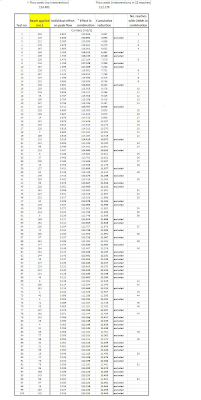
Table 1. The number of reaches in the Uck catchment where, if applied to 1 individual reach, a CRIM would decrease flood peak by more than 5, 1 and 0.1 cumecs.



Table 1 shows some of my initial results. It shows for example that, using the 30mm time map, there are 11 reaches which reduce the largest flood peak by over 5 cumecs individually. It can be seen that with increased rainfall rate, more reaches have a reducing effect on the main flood peak - this is not suprising as for the higher rainfall rates initial flood peak is higher.

-NOTE- It is also important to note that there are also many reaches which increase the flood peak when a CRIM is added, and many more 'neutral' sites where the effect is insignificant. In addition to this, for various reasons some of the reaches may not be suitable for CRIMs even if the model shows that increasing roughness in that area has a positive effect on flood reduction.
For example an area of floodplain may all ready be heavily vegetated - therefore floodplain roughness cannot be increased in practice.

The results are encouraging - when looking at a qualitatively good simulation of the 2000 flood hydrograph, over 50 reaches can potentially reduce the main flood peak by over 0.1 cumecs individually.

However there are other points to consider when looking at these results;

I was quite surprised at the extent of the effect of applying CRIMs to certain reaches, largely though not exclusively located along the main Uck. Four reaches reduced the flood peak by over 10 cumecs on their own. This is an extremely large reduction.
This may be due to a model artefact. - As an additional analysis I am going to run the same simulations again but this time not increase the channel rough as much;
The default channel roughness (represented as manning's roughness, n) is 0.035;
For the results discussed here, n was increased to 0.14;
This could be potentially too high so I'll run the same simulations again, increasing channel n to 0.08. This will represent a less extreme intervention and I hope results will still be positive;

Secondly so far I have only analysed my results looking at flood peak reduction. It is not necessarily helpful to reduce the flood peak if the volume of water above critical flood discharge - the amount of water spilling onto the floodplain - remains the same over a storm event. (Though it may still be beneficial in terms of timing of flood waters)

Therefore I need to look at the volume of water above critical flood discharge. This is proving to be more difficult for me to do than hoped. I basically need to figure out how to work out the area under a section of the discharge curve. This appears to be a slightly complicated proceduce and one I haven't figured out yet.

After looking at the individual effect of adding CRIMs, I will need to look at how combinations of CRIMs affect the flood peak.

Images showing my initial results to follow....

Ed

Sensitivity analysis - preliminary results

As discussed in the previous update, I aimed to carry out 2000 model runs to look at how the output (river discharge) of the model varied as model variables or parameters (such as channel roughness) were varied randomly.

The greatest difficulty with this has been just making sure that everything is set up correctly for my model runs. Sometimes this has involved quite a bit of trial and error - often a lot of model errors - to get everything right. As I can automate all my simulations it would be very annoying to find after 2000 simulations I'd made a msitake. However the simulations have now been carried out (with the help of Stuart letting me use his computer as well as mine).

I have used a number of different objective functions to analyse the accuracy of model predictions of the flood hydrograph. These basically attempt to quantify the goodness of fit of my observed (2000 flood event) and simulated hydrographs. Amongst these was the Nash-Sutcliffe model efficency (NSME), which allows measurement of the variation between the observed and the simulated hydrograph.

However Nash-Sutcliffe values were very poor for nearly all of the simulations. As were results showing the error in predicted flood peak. The low values were quite discouraging as it suggests that, at least when varying parameter values, the model is a poor respresentation of the observed flood hydrograph.

However there are several potential positives to take from the simulations;
- Firstly it is now even more clear that the model is very sensitive to rainfall rate applied. This stands to reason that a very small or very (very!) large rainfall rate is not likely to produce a flood hydrograph similar to that observed in 2000. - On reflection this is good in that it would be expected that the flood hydrograph would change quite considerably under different rainfall rates.

- Secondly the NSME statistic can give misleading results if they are not looked at closely.
For example it is biased towards the highest flows, therefore a model can be given a low NSME value even if most of the flood hydrograph is correctly predicted.
Also errors in the timing of flood peak can affect the results from using the statistic.
For example it is possible to produce a pretty good qualititative simulation of the observed hydrograph of the 2000 event using a set rainfall rate. From simply looking at this we can see that the timing of the peaks is slightly out - this can greatly affect NSME values. If the timing error if corrected for, very high NSME values can be achieved - indicating a good fit.

Therefore we believe the poor results are far from suggesting the model is not useful and it highlights the importance of not just analysing results but looking at how they are analysed.

As the model is very sensitive to rainfall rate only a small range of rainfall rate is likely to produce a good simulation of the flood hydrograph, therefore when I ran 2000 simulations very few combinations of variables produced 'good' results.

However after some extra thought usefull information can be found from the simulations. Trends in parameters values can be seen and will be looked at more closely in time. A future forward step is likely to be calibrating the model using several different rain rates as the event progresses. It is hoped this may offer up more accurate results and allow better investigation of the model parameters.

On the plus side it is now possible to run much faster simulations, using the computer power of several computers so results can be obtained much sooner.

Tomorrow I shall update you on results from my screening simulations, which are quite interesting.

Ed

New update soon...

New update coming soon...

Sensitivity analysis

Since my last message I have completed a number of steps in the modelling process.

I have been carrying out model sensitivity analysis for Overflow. Basically this process allows me to identify how the model behaves in terms of how important each variable or parameter is to the model behaviour. So far this process has been relatively exploratory.

The model contains a number of parameters such as;
• Channel, floodplain and catchment roughness values – set as Manning’s n values. Roughness affects conveyance
• Rain time maps
• Rainfall input
• Channel depth and width equations.

Each of these parameters has a default value. For example the channel network has a default Manning’s n value of 0.035. (For reference a Catchment Riparian Intervention Measure (CRIM), consisting of a debris dam and buffer strip, is likely to be given Manning’s n values of around 0.16 and 0.14 for the floodplain and channel respectively.)

My sensitivity analysis so far has involved varying the values of each key parameter one-at-a-time (OAT), whilst keeping the values of the other parameters fixed. A model simulation is run and the results recorded. Each simulation takes just under 10 minutes at the moment. The effect of varying each parameter on the model output (discharge) can then be analysed. The simulated discharge is seen to vary to a relatively high degree as a result of varying time maps and Manning’s n values; however it’s important to note that the parameters were varied over a large range.

The next step involves running simulations where every key parameter is varied at the same time, with values selected randomly. The results will show how the influence of each parameter relies on the interactions of the model parameters.

The ultimate aim of the above process is to narrow the range of potential values each parameter can take on, to identify and quantify the uncertainty in the model and its parameters.

Secondly I have run simulations where a CRIM is added to a single reach (234 separate reaches have been identified in the catchment). This is done by changing the Manning's n values of the reach to 0.16 for the floodplain and 0.14 for the channel. 234 simulations have to been run, with a CRIM added to a different reach each time. Whilst the sensitivity analysis is being carried out I will be able to have a first look at which locations it would be beneficial to add a CRIM, in terms of a reduction is peak flood discharge.

Again please feel free to email me with any questions you have at: edward.byers@durham.ac.uk. I hope to update the blog more frequently in order to allow readers a more detailed and better understanding of the development of my study.

Thanks, Ed

The Modelling Process

To all those interested:

The modelling process involved in the case of Uckfield, and in fact any similar study, is a long one with several important steps before any potential results can be achieved and analysed. It is also important that any results are viewed in the context of model uncertainty.

Therefore by updating you all on my progress, hopefully you will be able to understand and follow the steps that I take in the modelling process, as well as my masters study in general.

I am currently in the process of familiarising myself with the Overflow model. This involes gaining and developing a general understanding of how the model works through running basic instructions and looking at what output the model can provide. This learning stage is very important before I can look at the model more in-depth.

In addition to learning to use this model, as part of my masters degree, I am also developing a greater understanding of the more broad issues relating to the Uckfield case, particularly in terms of flood attenuation.

As allways, feel free to e-mail me with any questions you may have

Thanks, Ed

Some background to the study; my role and the wider context

As this blog may potentially reach a slightly wider audience I thought it appropriate to explain in more detail my study for those that are not aware of it:

Context

The town of Uckfield, Sussex experiences regular flooding, with the flood event in 2000 being particular large. In the subsequent flood report;

(http://www.wealden.gov.uk/Planning_and_building_control/Development_Control/Uckfield%20Appeals/WD-2006-2173/Water%20%28Drainage%20and%20Flood%20Risk%29/Appendix%20W6/Appendix%20W6%20-%20Extract%20from%20BBV%20Report%20on%20Sussex%20Ouse%20Flooding.pdf)

it was stated the rainfall in a 16 hour period of 11/12th October in the Uck catchment was estimated to be a 1 in 150 year event.


Further info on 2000 flood;
http://www.geography.org.uk/resources/flooding/Uckfield

Following this event, a flood wall was built to reduce flood risk for 30 properties, however this wall is expected to be designed for a 10-year event;
http://www.environment-agency.gov.uk/news/112405.aspx

My project comes at a time when there is much less money available for hard engineering approaches to flood protection such as large flood walls. There is also the realisation that such flood protection measures can have the effect of increasing flood risk downstream. In addition to this, in the event of flood wall failure, flooding can be even worse.

Therefore if it were possible to reduce flooding through the implementation of smaller-scale, diffuse, flood attenuation measures throughout the catchment this could potentially be very desirable.

For this study such measures will take the form of catchment riparian intervention measures (CRIMs). These CRIMs will most likely consist of a debris dam and riparian vegetation, with the aim of essentially slowing down water during high flow periods.

The idea behind the CRIMs is increasing the roughness of the channel and floodplain. Increasing channel roughness has the effect of reducing channel conveyance, causing small-scale local flooding. By increasing water storage in upstream areas of the catchment, the flood peak downsteam can potentially be reduced.

The hydrological model to be used is Overflow. The Overflow model is a reduced complexity model. The thinking behind use of such a model is that pysically-based models, for example SWAT, require a large number of parameters to represent physical properties of a catchment.

There is an uncertainty associated with each parameter - therefore such models may potentially be more uncertain than simpler models. A reduced complexity model also has the benefit of allowing relatively quick simulations to be carried out allowing quicker evaluation of interventions in the catchment.

My role in this study follows previous (and continuing) work with regards to the development of the model in Pickering and Uckfield, and also to the 'Knowledge Controversies' project:
http://knowledge-controversies.ouce.ox.ac.uk/

To summarise my role;

The aims of my masters research are:
1.To model the effects of CRIMs, placed throughout the catchment, on the flood peak downstream at Uckfield.
2. To evaluate the performance of a suitable reduced complexity model for assessing the impacts of small scale riparian woodland interventions
3. To develop an intervention strategy with the aim to reduce downstream flood risk, taking into account feasibility (e.g. biodiversity objectives)

Ed